
| Index A I | 構成・方式など |
|
SGD Optimizer 入力データ 誤差逆伝播法 勾配降下法 数値微分 勾配の算出 最適化問題 汎化能力 過学習 重みの初期値 多次元配列積 順方向伝播 連鎖率 アルゴリズム モデル フレームワーク 関数 レイヤー データ ハイパーパラメータ NN機能・要件 NN構成・方式 タスク 導入 Sample 用語 |
SGD (stochastic gradient descent、確率的勾配降下法) ・勾配方向へある一定の距離(ステップ幅 η(学習率))だけ進む。 確率を使って勾配の計算を高速に行う。 SGDクラス・ミニバッチ学習SGD 更新で使うデータ数を増やす。(16個、32個) 学習を遅くしてしまう要因の一つは、Pathological Curvatureで振動を起こす。・Momentum SGDの振動を軽減(SGDよりもジグザグが軽減) MomentumSGDクラス・AdaGrad パラメータの要素ごとに学習係数を調整する。 学習係数の減衰 過去の勾配を2乗和としてすべて記録 無限に学習すると更新量は0になる。 AdaGradクラス・Adam Momentumなどを融合 Adamクラス最適化アルゴリズム (Optimizer) ・全データを使ったバッチ学習では、まず全データの勾配を計算する。 全データの勾配の計算を並列化する。・確率的勾配降下法(SGD) 1つのデータで勾配を計算・更新し、次のデータで勾配を計算・更新する。入力データ ・バッチ処理 まとまりのある入力データ(batch)を一緒に処理 データ転送がボトルネックになりにくい。・入力データの投入方法 バッチ学習 (オフライン学習) オンライン学習 ミニバッチ学習誤差逆伝播法 ・重みパラメータの計算を効率よく行える。 ・連鎖率によって、局所的な微分を伝達する。 順伝播のメソッドを適切な順番で呼び出し、順伝播と逆の順番で逆伝播のメソッドを呼び出す。・連鎖率 合成関数(複数の関数で構成される関数)の微分において成立する関係式(性質) 合成関数の微分(導函数)は構成するそれぞれの関数の微分の積で表せる。 参考・加算ノードの逆伝播 入力された値(∂L / ∂z)をそのまま次のノード(複数)へ出力 加算ノード(加算レイヤ)の実装・乗算ノードの逆伝播 入力された値(∂L / ∂z)に順伝播入力をひっくり返した値を掛けて出力 乗算ノード(乗算レイヤ)の実装・ReLUレイヤ 順伝播入力がプラスの値なら、入力された値(∂L / ∂z)がそのまま出力、それ以外は「0」出力 ReLUレイヤの実装・Sigmoidレイヤ Sigmoidレイヤの実装・バッチ版Affineレイヤ バッチ版Affineレイヤの実装・SoftmaxWithLossレイヤ 損失関数、交差エントロピー誤差を含むSoftmaxレイヤ SoftmaxWithLossレイヤの実装勾配降下法(gradient descent method) ・直線の傾きを利用して関数の出来るだけ小さい値を探す。 ・現在の場所から一定の距離進み、再度勾配を求めることの繰り返し ・勾配法の数式表現(2変数の場合) \(x_{0}\) = \(x_{0} - η\frac{∂f_{}}{∂x_{0}}\) \(x_{1}\) = \(x_{1} - η\frac{∂f_{}}{∂x_{1}}\) \(η\)(イータ):学習率 更新の繰り返しで関数の値を減らす。 学習率は適切な値が必要
(ハイパーパラメータ)・勾配下降法の実装 def gradient_descent(f, init_x, lr=0.01, step_num=100): # x = init_x # for i in range(step_num): grad = numerical_gradient(f, x) #
勾配の実装 x -= lr * grad return x・関数 \(f(x_{0},x_{1})\) = \((x_{0})^2 + (x_{1})^2\)、初期値(-3.0, 4.0)の最小値を勾配法で求める。 勾配法の更新経緯の描画の実装 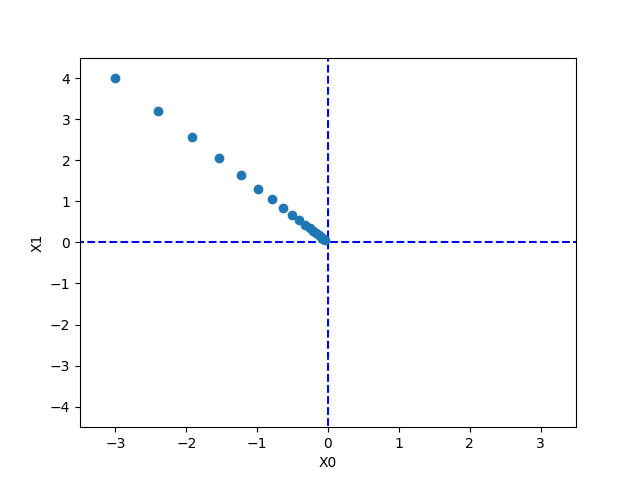 学習率が大きすぎると発散 学習率が小さすぎるとほとんど更新されない。数値微分 (numerical differentiation)方式 ・重みパラメータに関する損失関数の勾配を数値微分によって求める。 ・微分(導函数) 独立した変数に依存して決まるある量の変化の感度を測るもの 求める微分係数の直観的説明 関数のグラフのある点の接線の傾き ある点付近をグラフが直線に近づいて見えるまで拡大したときのその
直線の傾き 変数xの値の変化に伴うf(x)の変化を考えたとき、あるxにおけるf(x)の瞬間変化率 微分(参考)・数値微分実装 def numerical_diff(f, x): # 関数 f(x) = 0.01x**2 + 0.1x 、x = 10 h = 1e-4 # 0.0001 return (f(x+h) - f(x-h)) / (2*h) # df(x)/dx = 0.02x + 0.1 = 0.3 (直線の傾き)・偏微分実装 偏微分はターゲットとする変数以外を特定の値に固定 (新しい関数を定義し、その関数に数値微分関数を適用) 変数が2つの場合、新しい関数が2つできる。 関数「f(x0,x1) = x0**2 + x1**2」と数値微分の実装 >>> def function_2(x): ... return x[0]**2 + x[1]**2 >>> def numerical_diff(f, x): ... h = 1e-4 # 0.0001 ... return (f(x+h) - f(x-h)) / (2*h) ... 関数 f(x0,x1) で、変数 x0 = 3.0 (x1 を 4.0 に固定)の場合、の x0 の偏微分 >>> def function_tmp1(x0): ... return x0*x0 + 4.0**2.0 ... >>> numerical_diff(function_tmp1, 3.0) # ∂f / ∂x0 = 6 6.00000000000378 関数 f(x0,x1) で、変数 x1 = 4.0 (x0 を 3.0 に固定)の場合、の x1 の偏微分 >>> def function_tmp1(x1): ... return 3.0**2.0 + x1*x1 ... >>> numerical_diff(function_tmp1, 4.0) # ∂f / ∂x1 = 8 7.999999999999119・勾配(全ての変数の偏微分をベクトルとしてまとめたもの)の算出 2変数の関数 \(f(x_{0},x_{1}) = (x_{0})^2 + (x_{1})^2\) の
勾配の実装 2変数で表される各点の勾配を求められる。 勾配の結果にマイナスをつけたベクトル(矢印)の
描画の実装 勾配は一番低いところ(最小値)を指している。 一番低いところから離れると矢印が大きくなる。 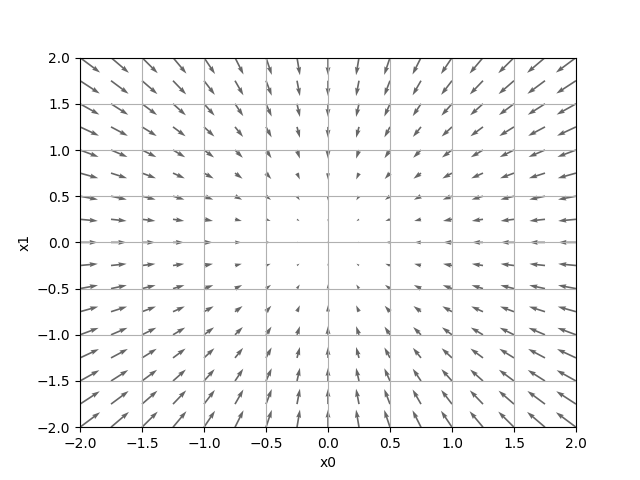 各所の勾配(両変数(全ての変数)の偏微分をベクトルとしてまとめたもの)が示す方向は、 各場所において関数 \(f(x_{0},x_{1})\) の値を最も減らす方向最適化問題 (optimization problem) ・与えられた関数に対し、出力値が最小または最大になる入力値を見つける。 損失 を下げる。 ヒント(勾配降下法)を使うと比較的簡単に下がる。汎化能力 ・まだ見ぬデータを正しく評価する。 過学習 ・訓練データだけに適応しすぎる。 ・過学習の主な原因 パラメータが大量で表現力が高いモデル 訓練データが少ない。・過学習を抑制 Weight decay (荷重減衰) 大きな重みをもつことに対してペナルティを課する。 Dropout ニューロンをランダムに消去しながら学習する。重みの初期値 ・重みを均一な値にすると、誤差逆伝播法ですべての重みの値が均一に更新される。 重みが均一になること崩す(重みの対称的な構造を崩す)ため、ランダムな初期値が必要・活性化関数の後の出力データ(アクティベーション)の分布で活性化関数との相性を確認 ・ReLU 「Heの初期値」を使用・sigmoid、tanh (S字カーブ) 「Xavierの初期値」を使用BatchNorm (Batch Normalization) ・各層でのアクティベーションの分布を適度な広がりを持つように調整する。 学習係数を大きくできる。 初期値にそれほど依存しない。 過学習を抑制する。・データ分布の正規化を行うレイヤをニューラルネットワークに挿入する。 多次元配列の積 ・行列の積では、対応する次元の要素数を一致させる。 正方行列として扱うと理解しやすい。(定理として証明しやすい。) 正方でない部分(欠落部分)には「0」を入れて正方行列にする。・行列式の定理 二つの(n, n)正方行列A、Bの積の行列式の値は、 Aの行列式の値とB行列式の値の積に等しい。・ numpy行列積 ListA(2次元・3要素)とListB(3次元・2要素)の行列積で ListAの要素数とListBの次元数が一致 一致しなければ、ValueError: shapes ・・・ニューラルネットワークの順方向伝播(forward propagation) ・ニューラルネットワークの「推論処理」 先に学習したパラメータを使い、入力データの分類を行う。推薦(recommendation) ・データの関連情報を導き出す。 次元削除(dimensionality reduction) ・データの特徴を残して削減する。 |
| All Rights Reserved. Copyright (C) ITCL | |