ニューラルネットワーク
  ・入力データを学習し、与えられた 探索問題 の 解決パターン を発生しようとする。
機械学習の有力な手法として発展。
訓練データを与え、入力と出力の相関（関数）を学習させる。
教師有り学習 方式のひとつ
  ・人の神経構造を模したアルゴリズム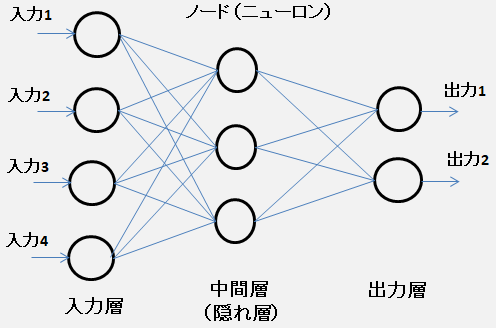

  ・出力層で人が望む結果が出るようにパラメータ（重みとバイアス）を調整する。
最適な重みパラメータをデータから自動で学習する。
損失関数の値をできるだけ小さくするパラメータを見つける 最適化問題
（単相の）パーセプトロンは適切な重みを人の手で決める。
  ・各ノード は単純な構成
  ・参考

入力
  ・決められた個数（図では4個）の 主に 0〜1 の範囲の実数
0〜1 の範囲で数値化できればなんでもよい
  ・画像
各ピクセルの RGB値 を個別の入力と考える。
画像 = ある個数の数値からなるベクトルと定義

出力
  ・決められた個数（図では2個）の 主に 0〜1 の範囲の実数
画像出もよい。

学習に必要なニューラルネットワークの条件
  ・学習の度合いの悪さを 損失（loss） として数値化できる。
損失は小さいほどよい。（損失 0 が最小）
  ・損失を表す関数（ 損失関数 ）が 微分可能（differentiable）
三層以上のニューラルネットワークは微分可の連続な任意関数を近似できる。
微分可能な変換を繋げて作られた計算グラフ
  ・ニューラルネットワークの学習では基本的に勾配降下法を使う。
勾配降下法では入力を少しずつ変化させながら解に近づいていく。
充分に実用的な結果が得られるまで処理を繰り返す。
完璧な解に到達できる保証はない。
  ・対象とする問題に関係なく、すべての問題を同じ流れで解ける。
勾配消失の課題をオートエンコーダの導入（2006年）で解決

ニューラルネットワークを多層化
  ・ディープニューラルネットワーク（DNN）
脳の仕組みを模したニューラルネットワークを多層に重ねたもの
  ・畳み込みニューラルネットワーク（CNN）
層間が全結合でない順伝播型ニューラルネットワーク
  ・再帰型ニューラルネットワーク （RNN）
時系列データを扱うことができるニューラルネットワーク
機械翻訳や音声認識に使用

ニューラルネットワークのロバスト性
  ・入力画像に小さなノイズが乗っても出力が変わらない頑強さ
ネットワーク内のデータを劣化させても出力結果への影響が少ない。
倍精度浮動小数点数→半精度浮動小数点数でも問題ない。
現GPU（32bit演算）が16ビット演算になれば、2倍の高速化